A familiar example is 1-dimensional polyacetylene (1). As is generally the case in one dimension, there are two Dirac points for polyactylene. Therefore a Dirac description of electron motion near each Dirac point is possible. A distortion of the underlying lattice (Peierls' instability) perturbes the electron motion in a way that couples the two Dirac points and opens a gap in the energy spectrum. In the Dirac equation description this is achieved by coupling the Dirac field ![]() to a scalar field
to a scalar field ![]() , which is a measure of the lattice distortion.
, which is a measure of the lattice distortion. ![]() enjoys a
enjoys a ![]() symmetry with two ground states in which it takes homogenous values
symmetry with two ground states in which it takes homogenous values
![]() . This coupling leads to a Dirac mass
. This coupling leads to a Dirac mass
![]() . But
. But ![]() can also take a position-dependent kink profile (soliton)
can also take a position-dependent kink profile (soliton) ![]() that interpolates between the two vacua
that interpolates between the two vacua
![]() . This ``twisting" of the mass parameter describes a defect in the lattice distortion. The Dirac equation with the kink profile
. This ``twisting" of the mass parameter describes a defect in the lattice distortion. The Dirac equation with the kink profile ![]() replacing the homogenous mass
replacing the homogenous mass
![]() possesses a single mid-gap (zero-energy) eigenstate. This gives rise to fractional fermion number for the electrons: 1/2 per spin degree of freedom (1).
possesses a single mid-gap (zero-energy) eigenstate. This gives rise to fractional fermion number for the electrons: 1/2 per spin degree of freedom (1).
Recently a similar story has been told by C.-Y. Hou, A. Chamon and C. Mudry (2) (HCM) about (monolayer) graphene. This is a 2-dimensional array of carbon atoms formed from a superposition of two triangular sublattices, A and B.
The generators of lattice A are
When no lattice distortion is considered, the tight-binding Hamiltonian, with uniform hopping constant ![]() , is taken as
, is taken as
![]() is diagonal in momentum space
is diagonal in momentum space
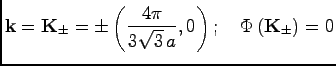
![]() is linearized around the two Dirac points,
is linearized around the two Dirac points,
![]() , and supplemented by a term arising from a (Kulé) distortion of the lattice; this couples the two Fermi points.
, and supplemented by a term arising from a (Kulé) distortion of the lattice; this couples the two Fermi points.
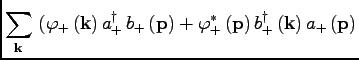 |
|||
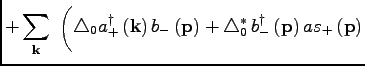 |
|||
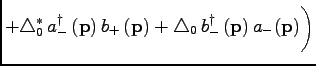 |
(5) |
To find zero modes for this system HCM promote the mixing parameter
![]() to an inhomogenous complex function
to an inhomogenous complex function ![]() with a profile like the scalar field in the Nielsen-Olesen-Landau-Ginsburg-Abrikosor vortex. To this end the Hamiltonian (5) is presented in coordinate spaces as
with a profile like the scalar field in the Nielsen-Olesen-Landau-Ginsburg-Abrikosor vortex. To this end the Hamiltonian (5) is presented in coordinate spaces as
![\begin{displaymath}
\Psi = \left(
\begin{array}{c}
\psi^b_+\\ [1ex]
\psi^a_+\\ [...
... d^2 k \, e^{-i {\bf p}\cdot {\bf r}}\, {b_{\pm}}\,({\bf p})$}
\end{displaymath}](img41.gif)
HCM take
![]() in the
in the ![]() -vortex form:
-vortex form:
![]() where n is an integer,
where n is an integer,
![]() vanishes as
vanishes as ![]() for small
for small ![]() , and approaches the mass-generating value
, and approaches the mass-generating value
![]() at large
at large ![]() . They then establish the occurrence of
. They then establish the occurrence of ![]() zero modes, i.e. solutions to
zero modes, i.e. solutions to
![]() , on lattice A (B) for negative (positive)
, on lattice A (B) for negative (positive) ![]() , and they construct explicitly the solutions for
, and they construct explicitly the solutions for ![]() . Therefore Fermion number
. Therefore Fermion number
![]() is fractionalized.
is fractionalized.