USAMTS Problem
Determine the smallest five-digit positive integer N such that 2N is also a five-digit integer and all ten digits from 0 to 9 are found in N and 2N.
First, we assume that a five digit number is greater than 10000; it does not start with 0.
We want to find the smallest such number, and for this we will start with the smallest possible numbers starting from the leftmost digits of N and 2N. Let us start with 1 as the first digit of N. This makes the first digit of 2N 2 or 3 and 2 is the smaller of these.
0 cannot be a digit of N because then its corresponding digit in 2N would either be 0 or 1, both of which are already taken.
The next smallest number we can use for the second digit of N is 3.
The next smallest number that we can use for the third digit of N is 4. Now that we have no more numbers less than 5 that we can use for N, there must be a carryover onto the third digit of 2N, making it be 9 instead of 8. By now, our numbers look like this:
N = 134??
2N = 269??
We still have not used numbers 5, 7, 8, and 0. (Remember, 0 cannot be used for a digit in N). The next smallest number we can use for the fourth digit of N is 5. However, there will be a carryover because there are no more available digits less than five, and the fourth digit of 2N would be 1, which we have already used.
The
next smallest number we can use for the fourth digit of N is 7. The fourth digit of 2N would then be 5. However, this leaves us with the numbers 8
and 0 for the last digits of N and 2N, and 28
= 16, whose last digit is not 0.
So,
our next smallest number which we can use for the fourth digit of N is 8. This would mean that the fourth digit of 2N
is 7. This leaves only 5 for the last
digit of N. 52
= 10. 0 would be the last digit of 2N,
and everything fits together perfectly.
So, the smallest numbers N and 2N such that the digits 0 through 9 are
used exactly once are:
N = 13485
2N = 26970
Note: I used cards numbered 0-9, and found one can systematically carry out this method in seconds. Actually, there are many more numbers N and 2N that satisfy the given requirements. In fact, if we consider numbers that begin with 0 five-digit numbers, then, by using the above procedure, we find that the smallest numbers N and 2N are:
N = 06729
2N = 13459
USAMTS Problem
It was recently shown that 2224 + 1 is not a prime number. Find the four rightmost digits of this number.
It is pretty easy to see that if a ≡ b (mod 10000), then a2 ≡ b2 (mod 10000). In other words, to obtain the rightmost four digits of x2, you don’t have to take the square of x. Instead, you just have to take the rightmost four digits of the square of the rightmost four digits of x. To prove this, let
x = 10000z + a,
where a is the last four digits of x, and z is a non-negative integer. Then:
x2 = (10000z + a)2
x2 = 100002z2
+ 2
10000
a
+ a2
Since the first two terms of the right hand side are divisible by 10000, they are not part of the last four digits of x2. So, the last four digits of a2 are the same as the last four digits of x2.
With this in mind, we can repeatedly take the squares of the last four digits, starting with 2 as shown in the table below. After 24 steps, we add 1, thus finding the last four digits of 2224 + 1.
|
22x ≡ |
... (mod 10000) |
|
21 ≡ |
2 |
|
22 or 22 ≡ |
4 |
|
24 or 42 ≡ |
16 |
|
28 or 162 ≡ |
256 |
|
224 or 2562 ≡ |
5536 |
|
225 or 55362 ≡ |
7296 |
|
226 or 72962 ≡ |
1616 |
|
227 or 16162 ≡ |
1456 |
|
228 or 14562 ≡ |
9936 |
|
229 or 99362 ≡ |
4096 |
|
2210 or 40962 ≡ |
7216 |
|
2211 or 72162 ≡ |
656 |
|
2212 or 6562 ≡ |
336 |
|
2213 or 3362 ≡ |
2896 |
|
2214 or 28962 ≡ |
6816 |
|
2215 or 68162 ≡ |
7856 |
|
2216 or 78562 ≡ |
6736 |
|
2217 or 67362 ≡ |
3696 |
|
2218 or 36962 ≡ |
416 |
|
2219 or 4162 ≡ |
3056 |
|
2220 or 30562 ≡ |
9136 |
|
2221 or 91362 ≡ |
6496 |
|
2222 or 64962 ≡ |
8016 |
|
2223 or 80162 ≡ |
6256 |
|
2224 or 62562 ≡ |
7536 |
2224 ≡ 7536 (mod 10000), so 2224 + 1 ≡ 7537 (mod 10000).
USAMTS Problem
Determine the integers a, b, c, d, and e for which
(x2 + ax + b)(x3 + cx2
+ dx + e) = x5 9x
27 .
Given
(x2 + ax + b)(x3 + cx2
+ dx + e) = x5 9x
27:
x5 + (a + c)x4 + (b + ca + d)x3 + (bc + ad + b)x2 + (bd + ea)x + be
= x5 9x
27
By comparing the coeficients of both sides, we get five equations:
a +
c = 0 (1
b +
ca + d = 0 (2
bc
+ ad + b = 0 (3
bd
+ ea = -9 (4
be
= -27 (5
1) gives:
c =
-a (6
2) gives:
b a2 + d = 0
or
d = a2 b
(7
3) gives:
-ba + a(a2 b) + e = 0
or e = ba a3 + ab
or
e = 2ab a3
(8
4) gives:
b(a2
b) + a(2ab
a3) = -9
or
a2b b2 + 2a2b
a4 + 9 = 0
or
a4 3a2b + (b2
9) = 0
(9
Solving for a2
a2
= (3b ± √(9b2
4b2 + 36))/2
or
a2 = (3b ± √(5b2
+ 36))/2
(10
From 5) we get:
be
= -27
, and since b and e are integers, b (and e) must be one of the following: ±1, ±3, ±9, or ±27.
To
find out which one will produce integer a, we will test each possibillity by
seeing if (3b ± /2 is a perfect square
and for that we check first (5b2 + 36) is a perfect square.
When b = ±1, 5b2 + 36 = 41, which is not a perfect square.
When
b = ±3, 5b2 + 36 = 81, which is a
perfect square, a2. (3b ± /2 = ±9 or 0, both of which are
perfect squares
When b = ±9, 5b2 + 36 = 441, which is a perfect square. However,
(3b
± /2 = ±24 or ±3, neither of which are perfect squares.
When b = ±27, 5b2 + 36 = 3681, which is not a perfect square.
The only possible values for b are 3 and -3.
If b = -3, a2 = -9 or 0
a2 = -9 is impossible because a is a real number.
a2 = 0 is also impossible because:
8) gives e = 2ab a3 = 0
or
be
= 0
but
from 5) we know that be
= -27.
So b cannot equal -3
Our only possibility is b = 3.
If b = 3, a2 = 9 or 0
We know a2 = 0 is impossible.
a2 = 9 is perfectly valid.
a = 3 or -3
b = 3
7) gives:
d = a2 - b
or d = 6
5) gives:
e = -27/b
or e = -9
4) gives:
bd + ea = -9
or 18 + -9a = -9
or a = 3
1) gives:
c = -a
or c = -3
Checking with our original five equations:
(1) 3 + (-3) = 0 true
(2) 3 + + 6 = 0 true
(3) (-9) + 18 + (-9) = 0 true
(4) 18 + (-27) = -9 true
(5) 3(-9)
= -27
true
a = 3
b = 3
c = -3
d = 6
e = -9
Thus:
(x2 + 3x + 3)(x3 3x2
+ 6x
9) = x5
9x
27
USAMTS Problem
A sequence of real numbers s0, s1, s2, ... has the property that
sisj = si + j + si
j
for all nonnegative integers i and j with i ≥ j,
si = si + 12 for all nonnegative integers i, and
s0 > s1 > s2 > 0.
Find the three numbers s0, s1, and s2.
Given:
sisj = si + j
+ si j
(1)
si
= si + 12
(2)
s0
> s1 > s2 > 0
(3)
When i = j = 0, (1) gives
s0s0 = s0 + s0
or (s0)2 = 2(s0)
Because s0 > 0, we can divide both sides by s0, getting
s0
= 2
(4)
We know that s12 = s0 (from (2))
When i = j = 6
(s6)2 = s12 + s0 = 2 + 2 = 4
s6 = ±2
Now (s3)2 = s6 + s0 = ±2 + 2 = {4 or 0}
Thus s3 = ±2 or 0
(5)
Now s2s1 = s3 + s1
or
s3 = s2s1 s1
s3
= s1(s2 1)
(6)
Since 0 < s2 < s1 < 2
|s1| < 2
|s2
1| < 1
so |s3| < 2
Thus, for s3 , 0 is the only possible value from (5),
s3
= 0 (7)
Since s1 ≠ 0, (6) gives
s2 = 1
Now, putting i = j = 1 in (1), we get
(s1)2 = s2 + s0 = 1 + 2 = 3
s1
= as s1 > 0
s0 = 2
s1 =
s2 = 1
Note: s3 = 0. We can easily calculate all values for si
eg:
s1 = s11 = ,
s2 = s10 = 1, s3 = s9 = 0, s4
= s8 = -1, s5 = s7 = -
,
and s6 = -2.
Since si = si + 12, we can find all values of si where i is an integer.
USAMTS Problem
|
|
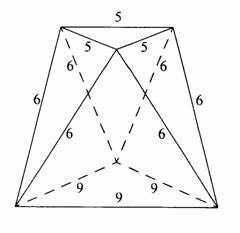
In the octahedron shown to the right, the base and top faces are equilateral triangles with sides measuring 9 and 5 units, and the lateral edges are all of length 6 units. Determine the height of the octahedron; i.e., the distance between the base and the top face.
|
|
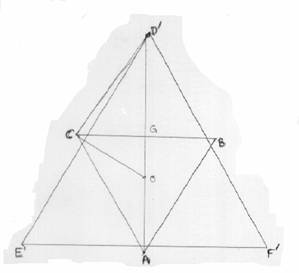
The given octahedron ABCDEF contains two equilateral triangles: equilateral ΔABC with sides measuring 5 units and equilateral ΔDEF with sides measuring 9 units. Lateral edges AE, AF, BD, BF, CD, and CE are congruent and have a measure of 6 units.
Let the midpoint of BC be G, the center of ΔABC be O (since it is an equilateral triangle, the circumcenter is the same as the incenter), and the center of ΔDEF be P.
In
an equilateral triangle (say, ΔABC) with center O
and sides measuring a, an altitude AG
= .
Since AO = BO = CO = 2OG
OG
=
(1)
(2)
We
see that GD' = OD' OG
and we also know that ΔCGD' is a right triangle,
so CD'2 = CG2 + GD'2
Also, ΔCDD' is a right triangle with side CD measuring 6,
so
the height DD' =
Now:
OG
= [Using
(1)]
(for
ΔD'E'F') OD' = [Using (2)]
Thus
GD' = OD' OG =
We know that CG = 5/2, so
CD'2
= CG2 + GD'2 = (5/2)2 + = 52/22 + (132
3)/62
= 61/3
Thus, height DD' =
=