USAMTS Problem 1/1/13
Determine the unique positive two-digit integers m
and n for which the approximation is accurate to seven decimals, i.e.,
.
Let us first take the reciprocal of our approximation for ,
that is,
. We get, to the nearest 7th digit,
4.2941179.
So, .
Again, we take the reciprocal of 0.2941179. This is approximately 3.3999974.
Now, .
Repeating these steps, we get
.
Simplifying this continued fraction, and neglecting the last number, we get
.
We verify that ,
which is indeed accurate to seven decimals, as required.
We also note that the first few convergents for 0.2328767 are
…
The next one has a numerator greater than 100, and is accurate only to four decimal places. Thus,
is the unique answer.
USAMTS Problem 2/1/13
It is well known that there are infinitely many
triples of integers (a, b, c) whose greatest common divisor is 1 and
which satisfy the equation . Prove that there are also infinitely many
triples of integers (r, s, t) whose greatest common divisor is 1 and
which satisfy the equation
.
Let us assume that r, s, and t are all greater than 0 (Not necessary integers), and if:
then dividing both sides by r2s2t2 we get
.
Now if this has a solution where r, s, and t are rational numbers (not necessarily integers) we can easily find an equivalent integer solution. (We multiply each term by a suitable number, as explained below)
But we do have such a solution, where ,
,
and
, and a,
b and c are integer solution of
!
In other words, suppose we have a primitive Pythagorean triplet (a, b, c).
Let ,
Now T, R, and S are not integers, but they are solutions of R2S2 + S2T2 = R2T2.
Then kR, kS, and kT are also solutions because if we multiply the above equation by k4 we get (kR)2(kS)2 + (kS)2(kT)2 = (kR)2(kT)2 .
Therefore, to find integer solutions, we choose: k = abc,
So that makes kR, kS, and kT each an integer.
So, {r = ac, s = ab, t = bc}
are the unique integer solutions for .
Also, we will prove that if (a, b, c) has a greatest common divisor of 1, then so does
(r, s, t).
If (a, b) have a common divisor k > 1, then let a = kx and b = ky.
Now, k2x2 + k2y2 = c2
This implies that k is also a factor of c, which means that (a, b, c) is not a primitive triple.
Similarly, any common factor of (a, c) will also be a factor of b.
Thus, no pair of (a, b, c) has any common factors greater than 1.
So, GCF(r, s) = a,
But there are no common factors greater than 1 with a and bc
Thus, GCF(r, s, t) = 1.
Since there are infinitely many solutions for (a, b, c), there are also infinitely many solutions for (r, s, t) by selecting r = ac, s = ab, and t = bc.
For example:
(3,4,5) gives a solution of (15, 12, 20), and
(5, 12, 13) gives us (65, 60, 156)
USAMTS Problem 3/1/13
Suppose for some angle x,
. Determine
for the same x.
It is easy to see that x ≠ 0, or π/2, so neither sin x or cos x is 0, hence it permissible to divide by sin x or cos x in all the following equations.
We will use
![]() and
and
=
.
or,
(eq
1)
Similarly,
(eq
2)
So, using eq 1 and 2,
and the fact that ,
we get
Since we are given that
USAMTS Problem 4/1/13
The projective plane of order three consists of 13 “points” and 13 “lines”. These lines are not Euclidean straight lines; instead they are sets of four points with the properties that each pair of lines has exactly one point in common, and each pair of points has exactly one line that contains both points. Suppose that points are labeled 1 through 13, and six of the lines are: A = {1, 2, 4, 8}, B = {1, 3, 5, 9}, C = {2, 3, 6, 10}, D = {4, 5, 10, 11}, E = {4, 6, 9, 12}, and F = {5, 6, 8, 13}. What is the line that contains 7 and 8?
We know that set G contains 7 and 8. Since each pair of points has only one line which contains both points, we know that no point which occurred in any other set that contained 7 or 8 may be contained in G.
Set A contains {1, 2, 4, 8}. Set F contains {5, 6, 8, 13}. This means that Set G must not have 1, 2, 4, 5, 6, or 13 as members. Thus, the only possible choices for the other two members are 3, 9, 10, 11.
The other two members can be 3, 9, 10, 11, and 12. One of these two points must be common to sets B, C, D, and E. However, these points must not both occur in any of these sets.
Checking all the possible combinations of these numbers: (3, 9), (3, 10), (3, 11),
(3, 12), (9, 10), (9, 11), (9, 12), (10, 11), (10, 12), and (11, 12) for this, we find that the possible pairs of points that do not both occur in any of the forementioned sets are:
(3, 11), (3, 12,) (9, 10), (9, 11), and (10, 12).
(3, 11) is not a possibility because set E contains neither of them.
(3, 12) is not a possibility because set D contains neither of them.
(9. 10) is a possibility because one of them is contained in each of the sets B, C, D, E, and F.
(9, 11) is not a possibility because neither of them is contained in set C.
(10, 12) is not a possibility because neither of them is contained in set B.
The only possible pair of points that can be in a set with 7 and 8 is (9, 10)
Thus, the only possible set G is {7, 8, 9, 10}
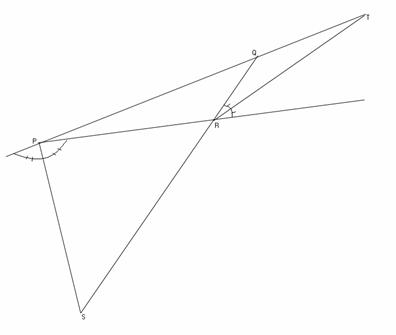 USAMTS Problem
5/1/13
USAMTS Problem
5/1/13
In PQR,
QR < PR < PQ
so that the exterior angle x V
bisector through P intersects
ray at point S, and the U
exterior angle bisector at R
intersects ray at
point T, as shown on the right.
Given that PR = PS = RT,
determine, with proof, the
measure of PRQ.
Let point U lie on in the opposite direction of T from P.
Let point V lie on in the opposite direction of P from R.
Let mPRQ
= x.
because it is supplementary to
PRQ.
Also, because PR = PS.
From we get
,
or
![]()
RPQ
is supplementary to
RPU,
so
,
or
Since RP = RT,
So,
QRV
is supplementary to
PRQ,
so m
QRV
= 180
x.
Thus,
From ΔQRT we get
,
or
Now, from ΔPQR, we get
,
or
Thus, mPRQ
= 132º