USAMTS Problem 1/1/14

 

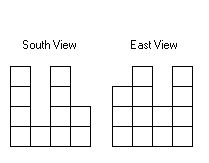
Some unit cubes are stacked atop a flat 4 by 4 square.  The figures show views of the stacks from two different sides.  Find the maximum and minimum number of cubes that could be in the stacks.  Also give top views of a maximum arrangement and a minimum arrangement with each stack marked with its height.

 

Diagramming the top view of the described figure, we have:

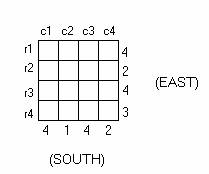
The apparent heights of each row and column are indicated at its relevant side.  (We define a “row” as the group of stacks that are behind a single east-projected stack and a “column” as the group of stacks that are behind a single south-projected stack.  Columns are labeled (c1, c2, …) from west to east, and rows are labeled (r1, r2, …) from north to south.)

 

To find the maximum number of blocks, we note that no stack in a given row or column can have a greater height than that indicated in its projection on the east and south sides. 

 

Thus, we can determine the maximum possible height for a given stack by taking the maximum heights possible for the row and the column that contains it, and taking the greatest value that satisfies both the row’s and the column’s height restriction.  In other words, when considering a given stack, we will take for its maximum possible height the lesser value of its two “projected” heights.

 

Following this procedure, we have:

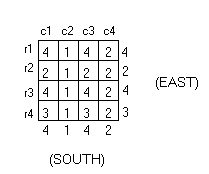
This is the arrangement utilizing the maximum number of blocks.  The numbers in each square represent the height of the stack occupying it.

 

The maximum number of blocks satisfying the given conditions is 38.

Redrawing the diagram for calculating the minimum arrangement,

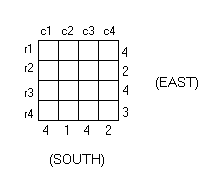
each row and column must have at least one stack which has the given height of its projection.  

 

To minimize the total number of cubes used, we want to use as few stacks as possible, preferably one per row or column, to generate the given projections’ heights. 

 

Let us start with c1.  We need at least one stack with height 4 in this column.  Because the east projections of r1 and r3 also have height 4, we could satisfy one of these rows’ requirements simultaneously with this column’s requirements by placing our stack of four cubes on the intersection of c1 and either r1 or r3.  In diagram below, we place this stack at (r1, c1).

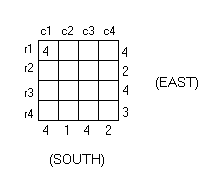
(Note that the stack could also have been placed at (r3, c1).  We are only finding one example of a minimum arrangement; however, there are other arrangements that will utilize the same, minimum number of cubes as this one will.)

 

Now, we will take c2, whose projection has height 1.  Because all the rows have projected heights greater than 1, it does not matter which row we place a stack of height 1 in for c2.  (Again, we are only finding one minimum arrangement.) We have:

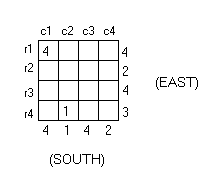
We can satisfy both c3 and r3’s requirements by placing a stack with height four at their intersection:

 

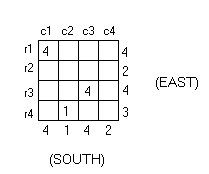
Similarly, we can satisfy the projected height requirements for c4 and r2 by placing a stack with height 2 at their intersection:

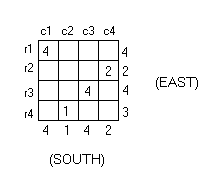
Now, r4 has the only projection which has not been satisfied.  There is no column with projected height 3; we can fulfill r4’s height requirement by placing a stack with height 3 in the intersection of r4 and either c1 or c3, which both have projected heights greater than 3:

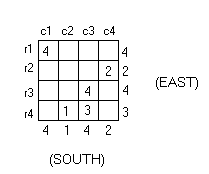
This is one possible arrangement that fulfils the given requirements with the minimum possible number of cubes.  There are 14 cubes used.

 

We can prove that this solution uses the fewest number of cubes possible; from the eastern projection, we know that there must be at least 4 + 2 + 4 + 3 = 13 blocks.  Also, we know from the southern projection that there is one stack with height 1.  So, there can be no less than 13 + 1 = 14 blocks.

USAMTS Problem 2/1/14

 

Find four distinct positive integers, a, b, c, and d, such that each of the four sums a + b + c, a + b + d,  a + c + d,  and  b + c + d  is the square of an integer.  Show that infinitely many quadruples (a, b, c, d) with this property can be created.

 

Let:      a + b + c = k2              (1)

            a + b + d = l2               (2)

            a + c + d = m2             (3)

and       b + c + d = n2              (4)

 

Adding (1), (2), (3), and (4), we get

 

or, a + b + c + d = .

 

Let  = S

 

Then:    S  k2 = d

            S  l2 = c

            S  m2 = b

            S  n2 = a

 

Since a, b, c, and d are distinct, so are  k, l, m, and n. (For example, if k = l it would imply that c = d.)

 

Now, if we can find k, l, m, n, such that:

  1. k, l, m, n are distinct positive integers.

Without loss of generality we can assume 0 < k < l < m < n

  1.  = S is an integer
  2. S
     n2 is positive   (This will make a, b, c, and d positive because n > m > l > k)

 

then we can find valid values for a, b, c, and d

 

Obviously, condition 2 can be satisfied if:

(a)    k, l, m, and n are all multiples of three, or

(b)   Exactly one of  is a multiple of three
(k2 ≡ 1 (mod 3) if k is not a multiple of 3)

 

For a simple case, let us take the case where k, l, m, and n are consecutive integers, and k is not divisible by 3.

That is,  is given by , and k is not divisible by 3.

 

Then, in (k2, l2, m2, n2), exactly one of the four terms is divisible by 3, and  is an integer.

 

We also need , or

k2 + (k +1)2 + (k + 2)2 > 2(k + 3)2

or 3k2 + 6k + 5 > 2k2 + 12k + 18

or k2  6k  13 > 0

k > 7.69… or k < -1.69…

 

k is a positive integer, so k > 7

 

Thus, the first possible consecutive  is (8, 9, 10, 11)

 

So,       k2 = 64

            l2 = 81

            m2 = 100

            n2 = 121

           

S =  = 122

 

d = S  k2 = 58

c = S  l2 = 41

b = S  m2 = 22

a = S  n2 = 1

 

(1, 22, 41, 58) is one example of  

 

There are infinitely many  ’s that are consecutive numbers where
k > 7 and is not divisible by 3.

 

So, there are infinitely many  ’s, and thus there are infinitely many  ’s.

 

[For example,   k = 8 gave the above solution for .

k = 10 gives:

S = 178,

a = 178  132 = 9

b = 178  122 = 34

c =  178  112 = 57

d = 178  102 = 78

  (9, 34, 57, 78)

            k = 11 gives:

S = 210

a = 210  142 = 14

b = 210  132 = 41

c = 210  122 = 66

d = 210  112 = 89

  (14, 41, 66, 89)

and so on.]

USAMTS Problem 3/1/14

 

For a set of points in a plane, we construct the perpendicular bisectors of the line segments connecting every pair of those points and we count the number of points in which these perpendicular bisectors intersect each other.  If we start with twelve points, the maximum possible number of intersection points is 1705.  What is the maximum possible number of intersection points if we start with thirteen points?

 

We assume that no two bisectors are common to each other, as this would result in “infinite points of intersection”.

 

If we start with x points, we will have  =  connecting lines, and thus also  perpendicular bisectors.

 

If we have n oblique lines with no restrictions on their placement, the maximum number of points of intersection that they can create is  = .

 

In our case, any 3 of the starting points form a triangle, and thus their perpendicular bisectors will all intersect at a single point.  This means that, for every set of three starting points, we will have a single point of intersection instead of 3 (given by  ). 

 

Thus, we must subtract  from the total possible number of points of intersection given by the formula  when n =  to get the correct answer.

 

Therefore, the maximum number of points of intersection for the perpendicular bisectors of  lines is:

 

 

 

So, when x = 12,

 =  = 1705

 

and when x = 13,

 =  = 2431

USAMTS Problem 4/1/14

 

A transposition of a vector is created by switching exactly two entries of the vector.  For example, (1, 5, 3, 4, 2, 6, 7) is a transposition of (1, 2, 3, 4, 5, 6, 7).  Find the vector X if S = (0, 0, 1, 1, 0, 1, 1), T = (0, 0, 1, 1, 1, 1, 0), U = (1, 0, 1, 0, 1, 1, 0), and
V = (1, 1, 0, 1, 0, 1, 0) are all transpositions of X.  Describe your method for finding X.

 

Entries cannot be added or removed; only switched; therefore, X must have four 1’s and three 0’s. 

 

For the first two entries, S has (0, 0, …) and V has (1, 1, …).  Since there is only one transposition, the only possibility is that:

 

X must have one 0 and one 1 among its first two entries.

 

This leaves two 0’s and three 1’s in the remaining five entries of X. 

 

Since the transposition from X to S (and also T) involves a 0 from the last five entries to the first two, any 0 in S (and also T) in the last five entries tells us that there is a 0 in its corresponding position in X.

 

The fifth entry of S is a 0, and the seventh entry of T is a 0.  Thus, the fifth and seventh entries of X are 0’s.  Since there are exactly two 0’s among the last five entries, all other entries among the last five entries of X are 1’s.

 

X can be either

(0, 1, 1, 1, 0, 1, 0)

or         (1, 0, 1, 1, 0, 1, 0)

 

If X is (0, 1, 1, 1, 0, 1, 0), exactly one pair of its entries can be transposed to form U. 

U =  (1, 0, 1, 0, 1, 1, 0).

The first two entries of X are transposed with respect to U.  However, so are the third and fourth entries.  This contradicts the condition that only one pair of entries can be transposed between U and X.

Thus, X cannot equal (0, 1, 1, 1, 0, 1, 0)

 

Thus, X = (1, 0, 1, 1, 0, 1, 0)

 

(X and S  have their first and seventh terms transposed.

 X and T have their first and fifth terms transposed.

 X and U have their fourth and fifth terms transposed.

 X and V have their second and third terms transposed.)

USAMTS Problem 5/1/14

 

As illustrated below, we can dissect every triangle ABC into four pieces so that piece 1 is a triangle similar to the original triangle, while the other three pieces can be assembled into a triangle also similar to the original triangle.  Determine the ratios of the sizes of the three triangles and verify that the construction works.

 


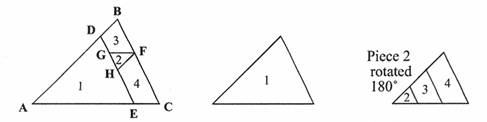
                        (Tri. X)                                            (Tri. Y)                                            (Tri. Z)

If , then:

 

 

 

, so .

Similarly, , so .

Also,  and , so .

(If you extend  to meet  at K then FKC = KFG, hence  )

 

Opposite sides of quadrilateral DBFH are parallel, that is, DBFH is a parallelogram.

Also, opposite sides of quadrilateral GFCE are parallel, so GFCE is a parallelogram.

 

Let GH = a.

 

In ,  and  are common.  So, GH = GD, and thus

GD = a.

 

DH = DG + GH, so

DH = 2a.

 

DH and BF are opposite sides of , so , and thus

BF = 2a.

 

In ,  and  are common.  So, HE = BF, and thus

HE = 2a.

 

GE = GH + HE, so

GE = 3a.

 

GE and FC are opposite sides of , so , and thus

FC = 3a.

 

DE = DH + HE, so

DE = 4a.

 

BC = BF + FC, so

BC = 5a.

 

Thus,    the ratio of corresponding side lengths for  and  is , or 3 : 4.

the ratio of corresponding side lengths for  and  is , or 4 : 5

and so the ratio of side lengths of , ,  is 3 : 4 : 5,

and the ratio of their areas is (32 : 42 : 52) :: (9 : 16 : 25).

 

(Note that 9 + 16 = 25, as it should be.)

 

It is easy to verify that this construction will always work, as we can draw  parallel to  (D is determined by the required ratio, that is AD : AB = 4 : 5), take a point F by dividing  at a ratio of 2 : 3, and draw lines  (parallel to  ) and  (parallel to  ). This will ensure that all the angles will be such that the pieces will fit and the triangles will indeed be symmetric.  (This is easy to check, using the properties of parallel lines).

 (parallel to  ) and  (parallel to  ). This will ensure that all the angles will be such that the pieces will fit and the triangles will indeed be symmetric.  (This is easy to check, using the properties of parallel lines).