USAMTS Problem 1/1/15
Let f(x) = for all real numbers x, where for any real
number r,
means the greatest integer less than or equal
to r. For example,
f(π) = 3 + 31 + 314 + 3141 = 3489. Find, with proof, a positive integer n less
than 2003 such that f(x) = n has no solution for x, but f(y) = n + 11 and f(z)
= n + 111 have solutions for y and z.
For any given real number x, let
a, b, c, and d are all integers, with b, c, and d greater than or equal to 0 and less than or equal to 9.
(When x is written in decimal form, a is the whole number to the left of the decimal point, and b, c, and d are the first three digits to the right of the decimal point.)
(We can show that b, c, and d are nonnegative integers less than or equal to 9
If we let ,
then 0 < z < 1.
,
so 0 < b < 9. The same is true for c and d.)
From the above definition,
f(x)
So, f(x) = n
n =
1111a + 111b + 11c + d.
Theorem:
Any integer n can
be written as for a unique integer set {p, r, t, u},
where:
In addition, when t = 10, u must equal 0,
and when r = 10, t and u must both equal 0.
Proof:
We divide n by 1111, and let p be the quotient and q be the remainder:
n = 1111p + q (0 < q < 1111)
We divide q by 111, and let r be the quotient and s be the remainder:
q = 111r + s (0 < s < 111, and 0 < r < 10; if r = 10, then s = 0)
Again, we divide s by 11, and let t be the quotient and u be the remainder:
s = 11t + u (0 < u < 11, and 0 < t < 10; if t = 10, then u = 0)
So, .
For f(x) = n to have no solution, one of {r, t, u} must equal 10.
The corresponding value from {b, c, d} will then not exist.
There are three such possible cases:
(1) r = 10 (In this case, t = u = 0)
(2) t = 10 (In this case, u = 0, and r is some value between 0 and 9)
(3) u = 10 (Both r and t are some value between 0 and 9)
We want to find a value for n such that f(x) = n has no solution,
but f(y) = n + 11 and f(z) = n + 111 both have solutions.
For case (1), we have
n = 1111p + 111(10) = 1111p + 1110
So,
n + 11 = 1111p + 1221
= 1111(p + 1) + 110
= 1111(p + 1) + 11(10)
That is, in this case we get t = 10. Therefore, f(y) = n + 11, too, has no solution.
Case (1) does not satisfy the requirements specified by the problem.
For (2), we have
n = 1111p + 111r + 11(10) = 1111p + 111r + 110
So,
n + 11 = 1111p + 111r + 121
= 1111p + 111(r + 1) + 10
That is, in this case u = 10. Therefore, f(y) = n + 11 has no solution.
Case (2) does not satisfy the requirements specified by the problem.
For (3), we have
n = 1111p + 111r + 11t + 10
So,
n + 11 = 1111p + 111r + 11t + 21
= 1111p + 111r + 11(t + 1) + 10
If 1 < t < 8,
then u = 10 and f(y) = n + 11 has no solution.
However, if t = 9, we have:
n + 11 = 1111p + 111r + 99 + 21
= 1111p + 111r + 120
= 1111p + 111(r + 1) + 9
We have a valid solution for f(y) = n + 11 for n where u = 10 and t = 9.
Also for (3), we have
n + 111 = 1111p + 111r + 11t + 121
= 1111p + 111(r + 1) + 11t + 10
If 1 < r < 8,
then u = 10, and f(z) = n + 111 has no solution.
However, if r = 9, we have:
n + 111 = 1111p + 999 + 11t + 121
= 1111p + 11t + 1120
= 1111(p + 1) + 11t + 9
We have a valid solution for f(z) = n + 111 for n where u = 10 and r = 9.
Therefore, in order to have a valid solution for f(y) = n + 11 and f(z) = n + 111,
we must have n where:
u = 10
t = 9
r = 9
That is, n = 1111p + 999 + 99 + 10
= 1111p + 1108
When p < 0,
n < 1108 1111, that is, n < -3
However, n must be positive, so p must be greater than or equal to 0
When p = 0,
n = 1108; there is no solution for f(x) = 1108
n + 11 = 1119; f(y) = 1119 when y = 1.008
n + 111 = 1219; f(z) = 1219 when z = 1.099
n = 1108 is a solution.
When p > 1,
n > 1111 + 1108, that is, n > 2219
However, in this problem, n must be less than 2003.
Thus, n = 1108 is the only possible solution.
USAMTS Problem 2/1/15
Find all primes p for which 6p + 1 is the fifth power of an integer. Prove that you found all of them.
,
so ,
where n is some integer.
We can factor n5
1 as
.
So, .
Since the factors of 6 are {6, 3, 2, 1}, we have eight possible cases:
When n = 1, ,
and when n > 2,
. So, cases 2, 4, 6, and 8 are impossible.
Taking case 1:
n 1 = 6, so n = 7, and
,
which is in fact prime.
For case 3, we have:
n = 4, and p = 341 / 2, which is not prime.
Similarly, for case 5, we have:
n = 3, and p = 121 / 3 which is not prime,
and for case 7, we have:
n = 2, and p = 31 / 6, which is not prime.
Thus, the only case which satisfies the given conditions is case 1, where n = 7 and p = 2801.
USAMTS Problem 3/1/15
We attempted to arrange the integers 1, 2, 3, …, 12 around a circle so that all sums of pairs of adjacent integers are either:
a) all perfect squares, or
b) all triangular numbers, which are numbers of the form n(n + 1) / 2.
One case out of (a) and (b) succeeded. Which one? For the successful case, show a valid arrangement. For the unsuccessful case, explain why it is impossible.
The sum of two different integers between 1 and 12
must be greater than or
equal to 3 (= 1 + 2) and less than or equal to 23 (= 11 + 12).
Case (a)
The perfect squares between 3 and 23 are {4, 9, 16}. In the list below are the possible integer pairs that can form perfect squares.
|
1 |
3, 8 |
|
2 |
7 |
|
3 |
1, 6 |
|
4 |
5, 12 |
|
5 |
4, 11 |
|
6 |
3, 10 |
|
7 |
2, 9 |
|
8 |
1 |
|
9 |
7 |
|
10 |
6 |
|
11 |
5 |
|
12 |
4 |
We note that for 2 (or, in fact, 8, 9, 10, 11, and 12), there is only one other number that it can sum with to form a perfect square.
If these numbers were arranged in a circle, each number would have two numbers adjacent to it, and thus would require at least two different numbers that it could sum with to form a perfect square. This is not the case; therefore, case (a) is impossible.
Case (b)
Now, the triangular numbers between 3 and 23 are {3, 6, 10, 15, 21}. In the list below, we have the possible integer pairs that can form triangular numbers.
|
1 |
2, 5, 9 |
|
2 |
1, 4, 8 |
|
3 |
7, 12 |
|
4 |
2, 6, 11 |
|
5 |
1, 10 |
|
6 |
4, 9 |
|
7 |
3, 8 |
|
8 |
2, 7 |
|
9 |
1, 6, 12 |
|
10 |
5, 11 |
|
11 |
4, 10 |
|
12 |
3, 9 |
Each number has at least two numbers with which it can sum to form a triangular number. Furthermore, we can arrange these numbers in a circle so that adjacent numbers always sum to form triangular numbers.
Let us start with 12: it must be adjacent to 3 and 9.
3 must be adjacent to 7.
7 must be adjacent to 8.
8 must be adjacent to 2.
So far, we have: (… 9, 12, 3, 7, 8, 2…)
12 must be adjacent to 9, and 6 must also be adjacent to 9, so 9 must lie between 12 and 6.
6 must be adjacent to 4, and 11 must also be adjacent to 4, so 4 must lie between 6 and 11.
So, we have: (… 11, 4, 6, 9, 12, 3, 7, 8, 2…)
11 must be adjacent to 10.
10 must be adjacent to 5.
5 must be adjacent to 1.
We have: (…1, 5, 10, 11, 4, 6, 9, 12, 3, 7, 8, 2…)
2 and 1 must be adjacent to one another. The arrangement can now form a circle. The arrangement is unique (ignoring inversion):

USAMTS Problem 4/1/15
Two players play a game. Each player, in turn, has to name a positive integer that is less than the previous number but at least half the previous number. The player who names the number 1 loses. If the first player starts by naming 2003 and after that both players play with the best strategy, who wins? Describe the strategy and prove it works.
We call a “winning number” any number which guarantees victory to the player who calls it.
If we have a winning number n, then 2n + 1 will also be a winning number because naming “2n + 1” forces the opposing player to name a number m, where n < m < 2n + 1. This means that the player who named “2n + 1” can always name n during his next turn, because n will be less than m, but greater than or equal to m / 2.
The player who names 1 loses. Therefore, 2 is a winning number, because the player who names 2 forces his opponent to name 1.
If 2 is a winning number, then so is 2(2) + 1 = 5. Recursively, we can continue finding a next-greatest winning number until we find the greatest one less than 2003. This is shown in the table below:
|
n |
2n + 1 |
|
2 |
5 |
|
5 |
11 |
|
11 |
23 |
|
23 |
47 |
|
47 |
95 |
|
95 |
191 |
|
191 |
383 |
|
383 |
767 |
|
767 |
1535 |
|
1535 |
3071 |
We find that 1535 is the greatest winning number less than 2003.
If player 1 names 2003, then player 2 can name 1535 because 2003 /2 < 1535 < 2003. 1535 is a winning number. Thus, as long as player 2 remembers his winning numbers, he will always win.
 USAMTS
Problem
USAMTS
Problem 5/1/15
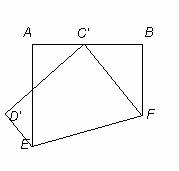
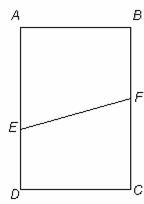
A rectangular piece of paper, ABCD, is folded along line segment EF, where point E is on side AD and point F is on side BC, so that C ends up at the midpoint of side AB. Determine the length of EF if the length of AB is 240 and the length of BC is 288.
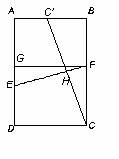 Let point G lie on
Let point G lie on such that
is perpendicular to
;
.
We will show that right triangle C’BC is similar to right triangle EGF, and thus calculate EF.
Let H be the
intersection of and
.
because they are symmetrical with respect to
the fold line,
so and
are perpendicular to each other.
is a right triangle, so
Also,
because
is perpendicular to
,
and thus also to
.
Therefore,
,
or equivalently
Taking and
,
we have
(both triangles are right triangles), and
.
Thus, .
BC = 288, and GF = AB = 240.
C’ is the midpoint of AB, so BC’ = 240 / 2 = 120.
So, ,
and GE = 100.
is a right triangle, so
EF = 260