USAMTS Problem 1/2/13
How many positive five-digit integers are there consisting of the digits 1, 2, 3, 4, 5, 6, 7, 8, 9, in which one digit appears once and two digits appear twice? For example, 41174 is one such number, while 75355 is not.
Each number that satisfies these conditions will consist of
three distinct digits, one which will appear once and two which will appear
twice. The number of ways to select
three digits out of nine is . In each set of three digits, any one digit (out
of 3) can appear a single time. Thus,
each case above will result in three possible combinations that can produce
five digits satisfying the above conditions.
So, we must multiply by 3 to obtain the number of possible ways to
select five digits consisting of three distinct digits satisfying the above
conditions.
We get .
Now, the number of ways we can permute 5 given distinct
digits is 5!. However, in our case, two
pairs of digits are identical. So, we
can arrange 5 given digits that satisfy the given conditions ,
or 30 ways.
Since, for each combination there are 30 permutations, and
since there are 252 combinations, there
are (252)(30),
or 7560 five digit numbers that satisfy the given conditions.
USAMTS Problem 2/2/13
Determine, with proof, the positive integer whose square is exactly equal to the number
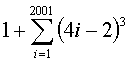
Let us take a general case .
So,
is the sum of the cubes of all odd numbers
from 1 to 2n. This can be written as the difference of the
sum of all cubes from 1 to 2n and the
sum of all even cubes from 1 to 2n. The sum of the cubes of all even numbers from
1 to 2n is
.
We will use the fact that ,
which can be proven by induction. (See http://www.shu.edu/projects/reals/infinity/answers/induct.html
and http://www.cse.ucsc.edu/classes/cmps102/Fall01/solutions2.pdf
for proofs.)
So,
So, when n = 2001,
S = (4(2001)2-1)2 = (16016003)2
USAMTS Problem 3/2/13
Factor the expression
If we expand an expression:
,
we get
So, the factored form of
will have coefficients w, x, y, z, k, l, m, n such that
From Eq. 1, we get
We can now write Eq.’s 2-7 in terms of w, x, y, and z:
,
or
,
or
Solving these quadratic equations, we get
Without loss of generality, we can assume that w = 1. (We can always divide the first factor by a constant and multiply the second factor by the same constant to make w = 1.
Now we have
x = 5/3 or 3/5
y = -1/2 or -2
z = -1/5 or -5
x/y = -5/6 or -6/5
x/z = -1/3 or -3
y/z = 2/5 or 5/2
So, if x = 5/3, then y = -2 and z = -5
If x = 3/5, then y = -1/2 and z = -1/5
Thus, the factors are
(1a + (5/3)b 2c
5d)(30a
+ 18b
15c
6d),
or
(1a + (3/5)b (1/2)c
(1/5)d)(30a + 50b
60c
-150d)
Multiplying and dividing by suitable constants to get integer coefficients, we get
(3a + 5b 6c
15d)(10a + 6b
5c
2d),
or
(10a + 6b 5c
2d)(3a + 5b
6c
15d)
These are the same, so the factorization of
is (3a + 5b
6c
15d)(10a + 6b
5c
2d)
We can verify that this factorization is correct by expanding it.
USAMTS Problem 4/2/13
Let X = (x1, x2, x3, x4, x5, x6, x7, x8, x9) be a 9-long vector of integers. Determine X if the following seven vectors were all obtained from X by deleting three of its components:
Y1 = (0, 0, 0, 1, 0, 1), Y2 = (0, 0, 1, 1, 1, 0), Y3 = (0, 1, 0, 1, 0, 1), Y4 = (1, 0, 0, 0, 1, 1),
Y5 = (1, 0, 1, 1, 1, 1), Y6 = (1, 1, 1, 1, 0, 1), Y7 = (1, 1, 0, 1, 1, 0)
We know that X has at least five 1’s because Y5 and Y6 have five 1’s. We also know that X has at least four 0’s because Y1 has four 0’s. So, since X has only 9 terms, there must be exactly five 1’s and four 0’s.
In Y1, 1 is the rightmost term. There are four 0’s to the left of it. Since there are only four 0’s in X, no 0 can be right of the 1 in X. Thus, the last term of X is 1. x9 = 1
In Y7, 0 is the rightmost term. There are four 1’s to the left of it. However, we know that the last term of X is 1, so the 0 must be followed by a 1. Since there are five 1’s in X, and four are to the left of the 0, there is only one 1 in front of the 0. Thus, the second-last term of X must be a 0. x8 = 0
Now, Y1 contains four 0’s. The rightmost 0 must be the second last term, because there can be no 0 to the right of it in X, and we know that there must be a 0 before the rightmost 1. There is a 1 to the left of this 0. Since there can be no more 0’s between this 0 and the 1 to the left of it, the third last term of X must be a 1. x7 = 1
In Y4, 1 is the leftmost term. There are three 0’s to the right of it. To the right of these three 0’s are two consecutive 1’s. Since X must end in (…1, 0, 1), the fourth 0 must either be between the two consecutive 1’s, or after the leftmost 1. In either case, it cannot be to the left of the leftmost 1. Since there are only four 0’s in X, no 0 can be left of the leftmost 1. Thus, the leftmost term in X is 1. x1 = 1
In Y2, both the leftmost and the rightmost terms are 0’s. The terms between these 0’s include three 1’s. There must be a 1 left of the leftmost 0 and a 1 right of the rightmost 0 in X. Since all our 1’s are now “used up”, and the term after the leftmost 0 in Y2 is also a 0, the leftmost 1 in X must be followed by two consecutive 0’s. Thus the second and third terms of X are 0’s. x2 = 0, x3 = 0
In Y7, there are four 1’s. Since the rightmost term is a 0, there must be a 1 to the right of it in X. Also, there must be two consecutive 0’s after the first 1 and before the second 1. Thus, the fourth, fifth, and sixth terms of X are 1, 0, and 1. x4 = 1, x5 = 0, and x6 = 1
We now have all nine components of X:
X = (1, 0, 0, 1, 0, 1, 1, 0, 1)
(It is easy to see that Y1, Y2, … Y7 can all be obtained by removing three components from X..)
USAMTS Problem 5/2/13
 Let R
and S be points on the sides
Let R
and S be points on the sides and
,
respectively, of
, and let P be the intersection of
and
. Determine the area of
if the areas of
,
, and
are 5, 6, and 7, respectively.
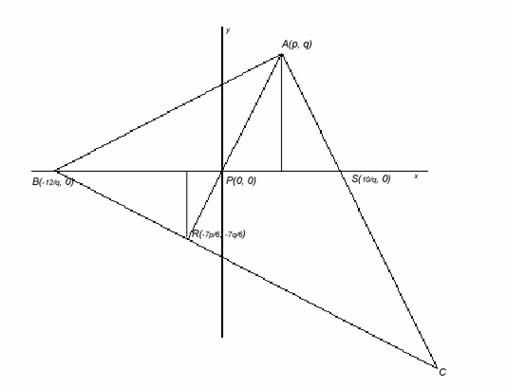
We place the figure on a coordinate plane, as shown
in the figure to the right. lies on the x axis, with P as
the origin. Let point A lie on (p, q).
Since the area of is 5, and
the height from to A
is q, the
length of must equal
.
Similarly, since the area of
is 6, the length of
must equal
.
Since the area of is 7, and
is
,
the height
of from
to R
must be
.
Since the triangle formed by ,
the altitude from A to
,
and the length from the altitude to P
is similar to the triangle formed by
,
the altitude from R to
,
and the length from the altitude to P,
the ratio of the lengths of the altitudes from R to
and from A
to
must be equal to the ratio of the lengths from
the altitudes to P. The length of the altitude from R to
is
,
and the length of the altitude from A
to
is q. Therefore, since the distance from the
altitude from A to
to point P
is p, the distance from the altitude
form R to
to point P
must be
.
Thus the coordinates of A, B, S, and R are A(p, q),
B( ,0),
S (
,
0), and R(
,
), with the origin at P.
The equation of the line is
,
or
,
or
,
or
The equation of the line is
, or
,
or
,
or
Lines and
intersect at point C.
So, for C(x, y),
and
,
so
,
or
,
or
,
or
,
or
,
or
So, point C lies 77q units below the x-axis.
The area of So, point C lies 77q units below
the x-axis. The area of So, (It is independent of p, q) The
area of is
. We know that BS is (
), and h
is (77
is
. We know that BS is (
), and h
is (77q).
is 858.