USAMTS Problem 1/3/15
Find, with proof, all pairs of two-digit positive integers ab and cd such that all the digits a, b, c, and d are different from one another and (ab)(cd) = (dc)(ba).
a, b, c, and d are decimal digits, distinct integers greater than 0 and less than or equal to 9.
(In this equation, “ac” is taken to mean the
decimal number with digits a and c, rather than
(ac)(bd)
= (dc)(ba), or the
multiplication of two numbers a and c.
Henceforth, we will denote multiplication of two digits with a “”
sign.)
(10a + c)(10b + d) = (10d + c)(10b + a)
So,
100a
c
+ 10
a
d
+ 10
b
c
+ b
d
= 100
b
d
+ 10
a
d
+ 10
b
c
+ a
c
99a
c
= 99
b
d,
or
ac
= b
d
We can find a finite (and small)
number of solutions for ac = b
d when a, b, c, and d are unique integers greater than 0 and less than or equal to
9.
There are only five numbers which can be factored into two four distinct decimal digits, or integers between 1 and 9, in two different ways.
6 (= 16,
2
3)
8 (= 18,
2
4)
12 (= 26,
3
4)
18 (= 29,
3
6)
24 (= 38,
4
6)
For each of these numbers, we can
let a equal any one of the four
factors, and b equal any one of the
factors in the pair that does not contain a. Thus, for each of these five numbers, there
are eight pairs {ab, cd}.
The 40 possible pairs {ab, cd} are listed on the next page, in
order of the ac = b
d value.
For ac = b
d = 6:
a = 1: a = 2:
{12, 63} {21, 36}
{13, 62} {26, 31}
a = 6: a = 3:
{62, 13} {31, 26}
{63, 12} {36, 21}
For ac = b
d = 8:
a = 1: a = 2:
{12, 84} {21, 48}
{14, 82} {28, 41}
a = 8: a = 4:
{82, 14} {41, 28}
{84, 12} {48, 21}
For ac = b
d = 12:
a = 2: a = 2:
{23, 64} {32, 46}
{24, 63} {36, 42}
a = 6: a = 3:
{63, 24} {42, 36}
{64, 23} {46, 32}
For ac = b
d = 18:
a = 1: a = 2:
{23, 96} {32, 69}
{26, 93} {39, 62}
a = 6: a = 3:
{93, 26} {62, 39}
{96, 23} {69, 32}
For ac = b
d = 24:
a = 1: a = 2:
{34, 86} {43, 68}
{36, 84} {48, 63}
a = 6: a = 3:
{84, 36} {63, 48}
{86, 34} {68, 43}
USAMTS Problem 2/3/15
Find the smallest positive integer n such that the product (2004n + 1)(2008n + 1) is a perfect square. Prove that n is as small as possible.
The values (2004n + 1) and (2008n + 1) have a difference of 4n. The greatest common factor of both (2004n + 1) and (2008n + 1) with 4n is 1. Thus, (2004n + 1) and (2008n + 1) have no common factors.
Since these two numbers are prime to one another, and when multiplied result in a perfect square, then they themselves must be perfect squares. So, (2004n + 1) and (2008n + 1) must each be perfect squares.
The number (2008n + 1) is odd. Therefore, its square root is also odd, and can be written as (2p + 1) for some integer p. So,
,
or
,
502 can be factored as 2(251). Thus,
,
and since 251 is prime, either p or p + 1 must have 251 as a factor. (We do not need to worry about 2 because either p or p + 1 will be a multiple of 2.)
So, values for n for which (2008n +1) is a perfect square will be of the form
,
with positive integer values for a for increasing multiples of 251. For each possible value of n for (2008n +1), we will check if that n also results in a perfect square value for (2004n +1)
When a = 1, n = 125 or 126
(2004(125) +1) = 250501, which is not a perfect square.
(2004(126) +1) = 252505, which is not a perfect square.
When a = 2, n = 501 or 503
(2004(501) +1) = 1004005, which is not a perfect square.
(2004(503) +1) = 1008013, which is not a perfect square.
When a = 3, n = 1128 or 1131
(2004(1128) +1) = 2260513, which is not a perfect square.
(2004(1131) +1) = 2266525, which is not a perfect square.
When a = 4, n = 2006 or 2010
(2004(2006) +1) = 4020025, which is a perfect square; it equals 20052
Thus, 2006 is the smallest value of n for which (2004n + 1)(2008n + 1) is a perfect square.
We see that and
;
thus
We can expect n = 2006 to work; in the solution for problem 4 of this round, we find that, when we multiply two numbers with a difference of two and add one, we have a perfect square, i.e., k(k + 2) + 1 = (k + 1)2.
It is interesting to see that we can find another solution for n from problem 4. In solving that problem, we find that when we have
a = k(k + 1)(k + 2)(k + 3) + 1,
then a is a perfect square.
Thus, another value of n would be n = (2005)(2006)(2007).
This will be a solution, because both
(2004)(2005)(2006)(2007) + 1 and
(2005)(2006)(2007)(2008) + 1
fit the form
k(k + 1)(k + 2)(k + 3) + 1,
and are thus both perfect squares.
So,
((2004)(2005)(2006)(2007) + 1)((2005)(2006)(2007)(2008) + 1)
would also be a perfect square.
However, the smallest value for n is 2006.
USAMTS Problem 3/3/15
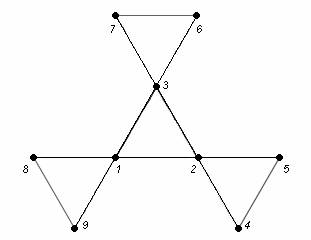 Pebbles
are put on the vertices of a combinatorial graph. For a vertex with two or more pebbles, a
pebbling step at that vertex removes one pebble at the vertex from the graph
entirely and moves another pebble at that vertex to a chosen adjacent
vertex. The pebbling number of a graph
is the smallest number t such that no matter how t pebbles are distributed on
the graph, the distribution would have the property that for every empty vertex
a series of pebbling steps could move a pebble to that one vertex. For example, the pebbling number of the graph
formed from the vertices and edges of a hexagon is eight. Find, with proof, the pebbling number of the
graph illustrated on the right.
Pebbles
are put on the vertices of a combinatorial graph. For a vertex with two or more pebbles, a
pebbling step at that vertex removes one pebble at the vertex from the graph
entirely and moves another pebble at that vertex to a chosen adjacent
vertex. The pebbling number of a graph
is the smallest number t such that no matter how t pebbles are distributed on
the graph, the distribution would have the property that for every empty vertex
a series of pebbling steps could move a pebble to that one vertex. For example, the pebbling number of the graph
formed from the vertices and edges of a hexagon is eight. Find, with proof, the pebbling number of the
graph illustrated on the right.
Let us label the vertices on the graph as shown, and let {n1, n2, n3, n4, n5, n6, n7, n8, n9} be the number of pebbles on each vertex {1, 2, 3, 4, 5, 6, 7, 8, 9}.
The number of pebbles that can move from one vertex to an
adjacent vertex is ,
where n is the original number of
pebbles on that vertex and [x] is the
greatest integer less than or equal to x.
Suppose we move the pebbles from vertices 4 and 5 to vertex 2. The resulting number of pebbles on vertex 2, N2, will be:
So,
Similarly, if we move the pebbles from vertices 6 and 7 at vertex 3, the resulting number of pebbles on vertex 3, N3, will have
Thus, after these moves, if we move the pebbles from vertices 2 and 3 to vertex 1, the resulting number of pebbles on vertex 1 N1 will be
,
or
So,
If ,
then N1 > 1, or N1 > 2.
Let us take 9 as the destination vertex. (Vertices {4, 5, 6, 7, 8, 9} are symmetric,
so it does not matter which one of these we choose. Vertices {1, 2, 3} are symmetric as well. However, it is easy to see that, if we can
reach a vertex in {4, 5, 6, 7, 8, 9}, we can also reach one of {1, 2, 3}. We have seen this in the above moves; we can
move at least one pebble to vertex 1 if .)
If N1 or n8 is greater than or equal to 2, then we can move pebbles onto vertex 9.
So, if > 12, or if n8 > 1, we can move pebbles onto vertex 9.
In the figure below is the combinatorial graph with 13 pebbles placed upon it. It is not possible to place a pebble on vertex 9 through pebbling steps. (The vertices are labeled in italics, and the initial number of pebbles on each vertex is given in bold.)
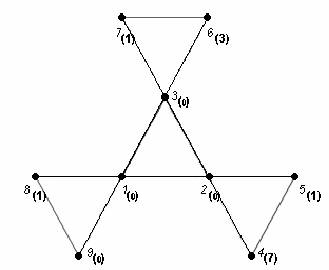
Thus, if n8 + n8 + n8 + n8 + n8 + n8 + n8 + n8 > 13, we can always move a pebble onto vertex 9. Furthermore, 13 pebbles is not enough to reach every vertex for every distribution. Thus, the pebbling number of this graph is t = 14.
USAMTS Problem 4/3/15
An infinite sequence of
quadruples begins with the five quadruples (1, 3, 8, 120),
(2, 4, 12, 420), (3, 5, 16, 1008), (4, 6, 20, 1980), (5, 7, 24, 3432). Each quadruple (a, b, c, d) in this sequence
has the property that the six numbers ab + 1, ac + 1, bc + 1, ad + 1, bd + 1,
and cd + 1 are all perfect squares.
Derive a formula for the nth quadruple in the sequence and
demonstrate that the property holds for every quadruple generated by the
formula.
We notice that a = 1 for the first quadruple, and increases by 1 for the following four quadruples. We will assume that a = n for the nth quadruple in this sequence.
For the first five quadruples, we notice that b = n + 2.
We will check if this fits the described properties of the sequence:
ab + 1 = n(n + 2) + 1 = n2 + 2n + 1 = (n + 1)2
This is a perfect square, so we will continue using these values for a and b.
For the first five quadruples, we notice that c = 4(n + 1)
Check:
ac + 1 = 4n(n + 1) + 1 = 4n2 + 4n + 1 = (2n + 1)2
bc + 1 = 4(n + 2)(n + 1) + 1 = 4n2 + 12n + 9 = (2n + 3)2
For the first five quadruples, we notice that d = 2(2n + 1)(2n + 2)(2n + 3)
(It is easy to see this pattern, but I actually took the successive differences, and found the fourth order difference to be 96, and thus found the pattern.)
Check:
ad + 1 = 2n(2n + 1)(2n + 2)(2n + 3) + 1
= (4n2 + 6n)(4n2 + 6n + 2) + 1
Let 4n2 + 6n = x; we have x(x + 2) + 1, which we have shown equals (x + 1)2.
= (4n2 + 6n + 1)2
bd + 1 = 2(n + 2)(2n + 1)(2n + 2)(2n + 3) + 1
= 4(n + 1)(n + 2)(2n + 1)(2n + 3) + 1
= 4(2n2 + 5n + 2)(2n2 + 5n + 3) + 1
Let 2n2 + 5n + 2 = x; we have 4x(x + 1) + 1, which we have shown equals (2x + 1)2.
= (4n2 + 10n + 5)2
cd + 1 = 8(n + 1)(2n + 1)(2n + 2)(2n + 3) + 1
= 4(2n + 1)(2n + 2)(2n + 2)(2n + 3) + 1
= 4(4n2 + 8n + 3)(4n2 + 8n + 4) + 1
Let 4n2 + 8n + 3 = x; we again have 4x(x + 1) + 1, which equals (2x + 1)2.
= (8n2 + 16n + 7)2
The nth term of (a, b, c, d) is (n, n + 2, 4(n + 1), 2(2n + 1)(2n + 2)(2n + 3).
USAMTS Problem 5/3/15
 In
triangle ABC the lengths of the sides of the triangle opposite
In
triangle ABC the lengths of the sides of the triangle opposite
to the vertices A, B, and C are known as a, b, and c, respectively.
Prove there exists a constant k such that if the medians
emanating from A and B are perpendicular to one
another, then a2 + b2 = kc2. Also find the
value of k.
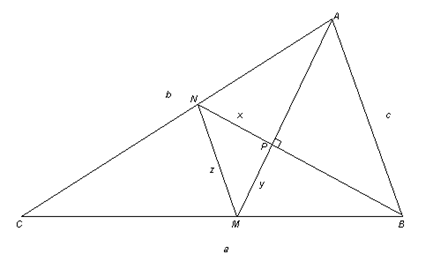
Let NP = x, MP = y, and MN = z, as shown in the figure above.
BN and AM are medians; thus, N and M are the midpoints of AC and BC, respectively. So,
and
.
Also, triangle NMC
is similar to triangle ABC because and
,
and angle C is common. Thus,
Triangles APN, BPM, NPM, and APB are right triangles. So,
Thus,
,
or
,
But, triangle NPM is a right triangle, so x2 + y2 = z2.
We know that . So,
,
or
Thus, we can write a2 + b2 = kc2, where k = 5.