USAMTS Problem 1/4/15
Find, with proof, the smallest positive integer n for which the sum of the digits of 29n is as small as possible.
Let m = 29n
Since 29 is prime to 10, the units digit of m must be greater than 0. Also, the leftmost digit of m by definition must be greater than 0.
So, the sum of the digits of m is greater than or equal to 2. In fact, the sum of the digits of m is 2 if and only if m is of the form (10k + 1).
We see that such a case does exist when k = 14. That is, 1014 + 1 is divisible by
29.
(See note below we can use Fermat’s Little Theorem to help
find this value.)
Thus, when n = (1014 + 1) / 29 = 3448275862069, we get m = 1014 + 1, and the sum of the digits is 2.
We have checked that for all values of k < 14, 10k
+ 1 is not divisble by 29. Thus,
n = (1014 + 1) / 29 is the smallest possible value for n.
Note:
Since 29 is prime, from Fermat’s Little Theorem, we know that:
1028 ≡ 1 (mod 29).
Let h be the smallest positive integer where
10h ≡ -1 (mod 29)
Then, 102h = 1 (mod 29)
So, 28 must be divisible by 2h, or 14 must be divisble by h.
We check the possible values of h 1, 2, 7, and 14, and find that h = 14 is the smallest number for which
10h ≡ -1 (mod 29)
USAMTS Problem 2/4/15
For four integer values of n greater than six, there exist right triangles whose side lengths are integers equivalent to 4, 5, and 6 modulo n, in some order. Find those values. Prove that at most four such values exist. Also, for at least one of those values of n, provide an example of such a triangle.
Let the triangle side lengths be:
an + 4
bn + 5
cn + 6
where a, b, and c are all nonnegative integers.
We have three cases, depending on which of these sides is the hypotenuse:
1: (an + 4)2 + (bn + 5)2 = (cn + 6)2
2: (an + 4)2 + (cn + 6)2 = (bn + 5)2
3: (bn + 5)2 + (cn + 6)2 = (an + 4)2
Modulo n, these reduce to:
or
1: 5 ≡ 0 (mod n)
Since n > 6, the possible values of n are (from 2) 9 and 27 or (from 3) 9, 15, and 45.
Thus, the possible values of n are 9, 15, 27, and 45.
(An example of such a right triangle, where n = 9, is
the Pythagorean triplet {24, 32, 40}
(or 8 × {3, 4, 5}). In this case, 24 =
(2(9) + 6), 32 = (3(9) + 5), and 40 = (4(9) + 4).)
USAMTS Problem 3/4/15
Find a nonzero polynomial f(w, x, y, z) in the four indeterminates w, x, y, and z of minimum degree such that switching any two indeterminates in the polynomial gives the same polynomial except that its sign is reversed. For example, f(z, x, y, w) = -f(w, x, y, z). Prove that the degree of the polynomial is as small as possible.
In the example above, indeterminates w and z
are switched, and we have
f(z, x, y, w)
= - f(w, x, y, z).
So, for ,
when w = z, ,
or
.
Thus, (w z) must be a factor of
.
Similarly, when w = x, when w = y,
when x = y, when x = z, and when y = z,
= 0.
Thus,
,
,
,
,
,
and
must all be factors of
.
So, a polynomial with this property with minimum degree has
factors
,
,
,
,
,
and
,
and can be expressed as:
.
USAMTS Problem 4/4/15
For each nonnegative integer n define the function fn(x) by
fn(x) = sinn (x) + sinn (x + 2π/3) + sinn (x + 4π/3)
for all real numbers x, where the sine function uses radians. The functions fn(x) can be also expressed as polynomials in sin (3x) with rational coefficients. Find an expression for f7(x) as a polynomial in sin (3x) with rational coefficients, and prove that it holds for all real numbers x.
f7(x) is defined as:
Expanding this, we have
or,
We know that
Since ,
and
,
USAMTS Problem 5/4/15
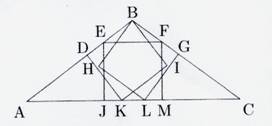 Triangle
ABC is an obtuse isosceles triangles with the property that three squares of
equal size can be inscribed in it as shown on the right. The ration AC / AB is an irrational number
that is the root of a cubic polynomial.
Determine that polynomial.
Triangle
ABC is an obtuse isosceles triangles with the property that three squares of
equal size can be inscribed in it as shown on the right. The ration AC / AB is an irrational number
that is the root of a cubic polynomial.
Determine that polynomial.
Let mBAC
= α (0° <
α <
45°), and let the side length of one of the inscribed squares
equal 1.
Then, AC = 1 + 2 cot α
and AB = 1 + cot α
AC / AB = x = 2 cos α
,
or
So,
Assuming that x ≠ 2 (if x = 2, α = 0), we have:
Thus, x = AC / AB is a root of 2x3
2x2
3x + 2 = 0.