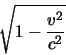


Next: Pretty Pictures
Up: Inessential LATEX
Previous: Foreign Symbols
Mathematical Text and other Special Symbols
Equations can be inserted into your text in several ways. Placing
$...$ or \(...\) or
\begin{math} ...\end{math} around the mathematical
expression or special symbol allows you to place it in a line of
normal text. This will use the smaller symbols (see
Figure 4), and adjust the size of the formula as
necessary. It will also adjust other things. For example, to place
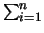 in a line of text, LATEX puts the ``i=1'' to the
right of the
in a line of text, LATEX puts the ``i=1'' to the
right of the  instead of underneath. Placing
instead of underneath. Placing
\[...\] or \begin{displaymath}...
\end{displaymath} around the expression will center it and set
it off from the rest of the text, using the larger symbols.
To create a simple equation, for example F=ma, you need only type
$ F=ma $. For more advanced formulæ, like E=mc2, you need
to tell LATEX to superscript the 2. The ^ character instructs
LATEX to superscript, and the _ character instructs LATEX to
subscript.
For example, $ E=mc^2 $ is used to produce E=mc2.
Likewise $ x_{k+1} $ is used to produce xk+1 .
If you want to put more than one character in the superscript or
subscript, you need to group them, using { and } as in
the examples above. To print something with both superscripts and
subscripts, like
238U+4, just type $ _{238}U^{+4}
$.21 Anything can
go into the brackets, and LATEX will figure out what to do with it:
x35+9<<880>>yz+4z1997 requires the hideous expression
$x^{35+9^{y_{z}}+4_{z}}_{1997}$, but if you look
carefully it should be clear what is happening.
To get the prime (') symbol in math mode, type an
apostrophe (').
Try some complex
expressions of your own, and see how easy they are to create. There are
many symbols not found on the keyboard to help you in formatting just
about any kind of formula. See Figures 5,
6, 7 and 8 for symbols
not found on the keyboard, like 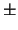 ,
,
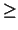 ,
and
,
and 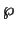 .
.
Figure 5:
Binary Operations
 |
Figure 6:
Relations
 |
Figure 7:
Arrows
 |
Figure 8:
Miscellaneous Symbols
 |
Of course, not all expressions are polynomials. LATEX uses two
special cases, \sqrt and \frac to create square roots
(radical sign surrounding the entire expression) and fractions (one
expression over another with a dividing bar between them)
respectively. The term
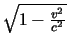 ,
commonly used in Lorentz transformations, is expressed as
,
commonly used in Lorentz transformations, is expressed as
$\sqrt{1-\frac{v^2}{c^2}} $ in line. You might want it displayed
as
instead, which is generated with
\[\sqrt{1-\frac{v^2}{c^2}} \].
If the equation is more interesting, or if you want to refer to it
later on, you might want to assign it a number by using the
equation environment. The quadratic formula
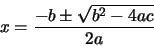 |
(1) |
is displayed by
\begin{equation}
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{equation}
You can supply an optional argument to \sqrt, specifying a
different root than 2. For example, the fourth root,
![$\sqrt[4]{1024}$](img53.gif) ,
is expressed as
,
is expressed as \sqrt[4]{1024}.
Often in a mathematical equation you will want to use symbols instead
of the standard italicized letters for variable names. You can add
Greek letters by typing the command associated with the particular
letter--see Figures 9 and 10.
Figure 9:
Lowercase Greek
|
Figure 10:
Uppercase Greek
 |
Note that if you want to use Greek letters in normal text mode, you
must place them in a math environment by surrounding them with
$...$. You can also create function names with the
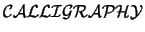 font. This is treated like any type style change
such as
font. This is treated like any type style change
such as \bf, but like the Greek letters, you can use it only in
math mode. In addition, you only have the 26 upper-case letters
available (see Figure 11).
Figure 11:
Calligraphic Symbols
 |
Sometimes, a formula contains text that should be set in roman type.
For example, in the formula ``
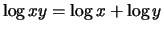 ,'' the word
``log'' is not italicized like the variables x and y. It would be
inconvenient to have to exit math mode to type the text in normal roman
type, so the most common function names are defined as special commands.
If the desired command isn't defined, you can use something like
,'' the word
``log'' is not italicized like the variables x and y. It would be
inconvenient to have to exit math mode to type the text in normal roman
type, so the most common function names are defined as special commands.
If the desired command isn't defined, you can use something like
$x = \textrm{foo}$ to produce
x = foo rather than x =
foo. A
formula such as
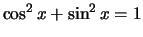 would be entered as
would be entered as
$\cos^2 x + \sin^2 x = 1$. See Figure 12 for a
list of all the special commands which are typeset like this.
The modulo function is slightly different from the other special
commands--it has two forms, a binary and a parenthesized one. See
Figure 13 for an example of their usage. There are also various
types of brackets and other delimiters available in math mode, as shown in
figure 14. Certain accents and other diacritical marks are
available in math mode. Some of these math mode accents are only
available in math mode, while others are modified to work better in
math mode.
See Figure 15 for examples.
Figure 12:
Log-like symbols
 |
Figure 13:
Modulus functions
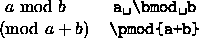 |
Figure 14:
Delimiters
 |
Figure 15:
Math-mode accents
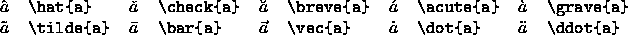 |
The symbols in Figure 16 were provided by LATEX 2.09, but not by
LATEX2e. You can access them by using the latexsym package.
Figure 16:
Symbols available in the latexsym package
|



Next: Pretty Pictures
Up: Inessential LATEX
Previous: Foreign Symbols
Alex Rolfe
1999-10-29