Chiral Gauge Theory for Graphene

In this paper we elaborate the HCM model, and address the following two topics. HCM leave unspecified the dynamics that give rise to the complex vortex profile.First we propose using the NOLAG vortices, which are described by a charged scalar field is in the HCM model. An $U (1)$ gauge field is also involved in creating the NOLAG vortex, but no gauge field is present on the HCM model. Therefore, second, we propose to couple the relevant gauge potential to the Dirac fermions in a chiral manner, so that, expanding the symmetry of the interaction, we render the theory invariant against local, chiral $U (1)$ gauge transformations, which also act on the scalar and Dirac fields. Additionally there remains a global fermion number $U (1)$ symmetry, and its charge is fractionalized.

To present our extension of the HCM model, we shall use Dirac matrix notation. We begin by rewriting 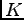$K$ in (7) in terms of Dirac matrices whose forms we take as follows.

$${\boldsymbol \alpha}= (\alpha^1, \alpha^2, \alpha^3) = {\boldsymb... ...0 \choose 0\, -\boldsymbol \sigma } \qquad \beta = {0\quad I \choose I\quad 0}$$

Note: we use 4x4 Dirac matrices, even though the minimal Dirac algebra in (2+1)-dimensions requires only 2x2 matrices. But we have four degrees of freedom: two each in lattices A and B. Since there are two spatial dimensions, we use only the first two $\alpha$ matrices : $\alpha^i , i = 1,2$ or $x, y$; we rename the third one, $\alpha^3$, as M. Also unlike with minimal 2x2 Dirac matrices, here we can construct the chiral $\gamma_5$ matrix, as the Hermitian quantity

$$\gamma_5 = -1 \alpha^i\, \alpha^2\, \alpha^3 = {I\quad 0 \choose 0\, -I}, \gamma^2_5 = I$$

The covariant $\gamma-matrices$ read

$${\boldsymbol \gamma}= \beta\, {\boldsymbol \alpha}= {0\,-\boldsym... ...gamma^0 = \beta,\quad \gamma_5 = i\, \gamma^0\, \gamma^1\, \gamma^2\, \gamma^3$$

Note that $C\equiv \alpha^3$ anti-commutes with $\beta$ and $\alpha^i (i=1,2)$, but it commutes with $\gamma_5$; the latter also commutes with $\alpha^i$, but anti-commutes with $\beta$.

With these matrices 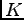$K$ in (7) may be presented as

$$\Psi^\ast\, K \psi = \psi^\ast\ ( {\boldsymbol \alpha}\cdot {\bf k}+ g \beta \ [\varphi^R - i \varphi^I\, \gamma_5 ] )\ \Psi$$ (8)

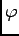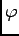Here ${\bf r}$ is operator $-i {\boldsymbol \triangledown}$; we have renamed $\triangle$ as $g \, \varphi$, where $g$ is a coupling strength and $\varphi$ is a complex scalar field, with real and imaginary parts: $\varphi = \varphi^R + i\, \varphi^I$. Note that when $\varphi$ is decomposed into modulus and phase: $\varphi = \mid\varphi\mid\, e^{i \chi}$, the interaction part of (8) may be presented as $g \mid\varphi\mid\, \Psi^\ast \, \beta\, e^{-i \gamma_5 \chi}\, \Psi$. This makes it clear that this interaction is invariant against the local chiral gauge transformation.

$$\varphi \to e^{2 i \omega}\, \varphi \Rightarrow \quad \chi \to \chi+ 2\omega$$

$$\Psi \to e^{i \omega \gamma_5}\, \Psi$$ (9)

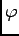[When $\varphi$ is constant, its constant phase may be removed from K by the above transformation, leaving a conventional Dirac mass term (gap). ]

In order that the kinetic portion of (8) be invariant against the local gauge transformation (9), we introduce coupling to a gauge potential 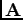${\bf A}$, which transforms as

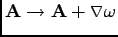$${\bf A}\to {\bf A}+ {\boldsymbol \triangledown} \omega$$ (10)

Thus our final Dirac Hamiltonian reads

$$\Psi^\ast \, K_A \, \Psi = \Psi^\ast\, {\boldsymbol \alpha}\cdot [{\bf p}- \gamma_5\, {\bf A}] \ \Psi\hspace{.75in}$$

$$+ g \Psi^\ast \beta \, [\varphi^R - i\, \gamma_5\, \varphi^I ] \Psi$$

$$=\bar{\Psi}_+\, {\boldsymbol \gamma}\cdot ({\bf p}- {\bf A}) \ \Psi_+ + \psi_- \, {\boldsymbol \gamma}\cdot ({\bf p}+ {\bf A}) \psi_-$$

$$+ g \, \varphi\, \bar{\boldsymbol \psi }_+ \, \psi_- + g \varphi^\ast\, \bar{\boldsymbol \psi }_- \, \psi_+$$ (11)

We have introduced the Dirac adjoint $\bar{\Psi} \equiv \Psi^\ast\, \gamma^0$, and the chiral components $\Psi_\pm \equiv \frac{1}{2} \ (1 \pm \gamma_5) \ \Psi$, whose gauge transformation law is

$$\Psi_\pm \to e^{\pm i \omega}\ \Psi_\pm , \quad \bar{\Psi}_\pm \to \bar{\Psi}_\pm\, e^{\mp i \omega}$$ (12)

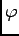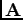The Bose fields $\varphi$ and ${\bf A}$ are determined by the familiar NOLAG equations

$${\bf D}\cdot {\bf D}\, \varphi = \varphi V^\prime \, (\varphi^\ast \, \varphi)$$

$${\bf D}\, \varphi \equiv (\triangledown - i\, 2 {\bf A})\ \varphi$$ (13)

$$\frac{1}{e^2}\ \varepsilon^{ij}\, \partial_j\, B = j^i_{\mbox{\tiny {BOSE}}}$$ (14)

$$B = \varepsilon^{ij}\, \partial_i\, A^i$$

$$j_{\mbox{\tiny {BOSE}}} = 4 \, I m \, \varphi^\ast\, {\bf D}\, \varphi$$

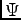Here $e$ is a further coupling constant and the potential $V$ is chosen so that at minimum $V^\prime = 0\, \varphi^\ast\, \varphi = \varphi^2_0$, which gives rise to the Dirac mass for $\Psi$. Furthermore, vortex solutions to these equations also exist. Their form is

$$\varphi\, ({\bf r})= \varphi\, (r)\, e^{i n \theta}$$

$$A^i\, ({\bf r})= -n \, \varepsilon^{ij}\, \frac{r^j}{r^2}\ a\, (r)$$ (15)

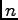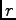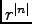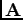where $n$ is an integer; $\varphi (r)$ vanishes with $r$ as $r ^{\vert n\vert}$ and tends to $\varphi_0$ at infinity; $a (r)$ vanishes at the origin so that ${\bf A}$ is regular there and tends to 1/2 at large 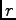$r$. All this ensures finiteness of the vortex energy $\int d^2\, r \left(\frac{1}{2e^2}\ B^2 + {\bf D}\, \varphi \mid^2 +\, V^\prime \, \varphi^\ast \varphi\right)$.

Finally, note that our system possesses a global fermion number symmetry, with just the Fermi fields transforming with a constant phase: $\Psi \to e^{i\lambda}\, \Psi$. Consequently the theory possesses a local chiral U(1) symmetry and a global U(1) fermion number symmetry. Because the theory resides in (2+1) dimensions, no chiral anomalies interfere with our chiral gauge symmetry.

Indeed, in spite fo the presence of the $\gamma_5$ matrix, the theory in parity (P) and charge-conjugation (C) invariant. This is because in (2+1) dimension, with 4-component Dirac fields the relevant transformations read

$$P: \varphi \ (t, x, y) \to A^{0, y}\ (t, -x, y)$$

$$y: A^{0, y}\ (t, x, y) \to - A^\ast\ (t, -x, y)$$

$$\Psi\, (t, x, y) \to i\, \gamma^3\, \gamma^\ast\, \Psi\ (t, -x, y)$$ (16)

$$C: \varphi \to \varphi^\ast$$

$${\bf A}\to - {\bf A}$$

$$\Psi_i \to \gamma^1_{ij}\, \bar{\Psi}_j$$ (17)