


Next: Energy Relations
Up: Chiral Gauge Theory for
Previous: Chiral Gauge Theory for
With the additional gauge potential 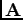 , our Dirac eigenvalue problem differs from HCM. From (11) we have
, our Dirac eigenvalue problem differs from HCM. From (11) we have
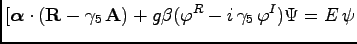 |
(18) |
Observe that
 anti-commutes with all the matrices on the left side of (16). Therefore if
anti-commutes with all the matrices on the left side of (16). Therefore if 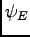 is an eigenfunction with eigenvalue
is an eigenfunction with eigenvalue 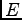 ,
, 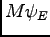 belongs to eigenvalue
belongs to eigenvalue 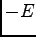 , and zero modes can be chosen as eigenstates of
, and zero modes can be chosen as eigenstates of 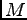 .
.
Next we show that the gauge interaction in (16) does not affect the zero modes found by HCN at
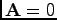 . To this end, we adopt the Coulomb gauge and present
. To this end, we adopt the Coulomb gauge and present 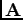 as
as
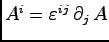 . Also it is true
. Also it is true
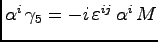 . Thus the kinetic term in (16) also is
. Thus the kinetic term in (16) also is
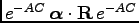 and (16) becomes
and (16) becomes
![$\displaystyle ({\boldsymbol \alpha}\cdot {\bf R}+ g\, \beta\, [\varphi^R - i \, \gamma_5\, \varphi^I]) \quad (e^{-AM}\, \Psi) \quad =\quad E\ (e^{AM} \, \Psi)$](img121.gif) |
(19) |
and
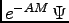 satisfies the HCM equation at
satisfies the HCM equation at 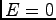 . Comparison with (15) shows that
. Comparison with (15) shows that
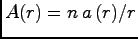 , so that the infinity
, so that the infinity
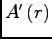 lends to
lends to
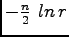 , and the zero modes with the gauge interaction differ from the HCM modes by factors
, and the zero modes with the gauge interaction differ from the HCM modes by factors
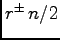 . This does not affect nomalizability because the zero modes are exponential damped by the interaction with
. This does not affect nomalizability because the zero modes are exponential damped by the interaction with 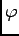 . Finally, since the HCN mode as well as ours has the form for
. Finally, since the HCN mode as well as ours has the form for
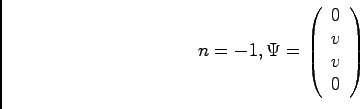 , we see that indeed it is an
, we see that indeed it is an 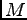 eigenstate, with eigenvalue
eigenstate, with eigenvalue 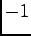 . Fermion number fractionalization in the gauge theory is now established by the same reasoning as in HCM.
. Fermion number fractionalization in the gauge theory is now established by the same reasoning as in HCM.



Next: Energy Relations
Up: Chiral Gauge Theory for
Previous: Chiral Gauge Theory for
Charles W Suggs
2007-05-07
![]() . To this end, we adopt the Coulomb gauge and present
. To this end, we adopt the Coulomb gauge and present ![]() as
as
![]() . Also it is true
. Also it is true
![]() . Thus the kinetic term in (16) also is
. Thus the kinetic term in (16) also is
![]() and (16) becomes
and (16) becomes
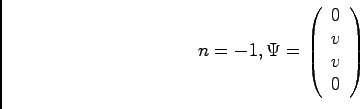 , we see that indeed it is an
, we see that indeed it is an