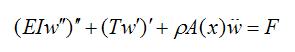|
||
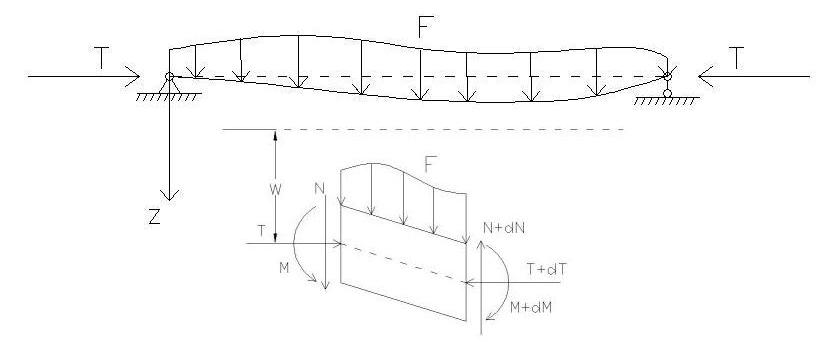
Mathieu Equations are encounted in many physics and engineering problems, such as diffraction, amplitude distortion, inverted pendulum, stability of a floating body, etc. Mathieu equation is a linear second-order differential equation with periodic coefficients, and (according to Wikipedia, "Mathieu Wavelet") it was first introduced by French mathematician, E. Léonard Mathieu, in his “Memoir on vibrations of an elliptic membrane” in 1868. In our flexible cylinder VIV experiment, I am interested in the axial force fluctuation caused by the VIV and its influence on the lateral response(CF and IL direction). The mechanical model and its typical volume unit goes:
And the equilibrium equation goes:
|
And at last when:
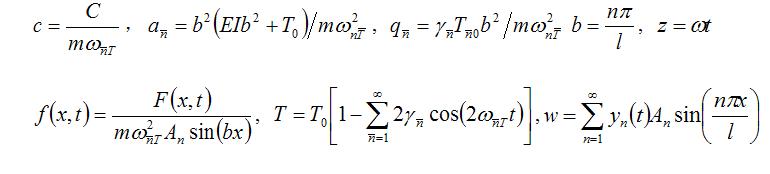 |
|---|
It goes form of Mathieu Equation:
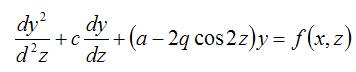 |
|---|
The Mathieu Equation is governed by Character a and q(the solution of the equation may be stable or unstable, periodic bounded or non periodic unbounded, which depends on the characters of a and q), and the Stability Chart of Mathieu Equations goes(Graphics from NIST Digital Library of Mathematical Functions, Handbook of Mathematical Functions):
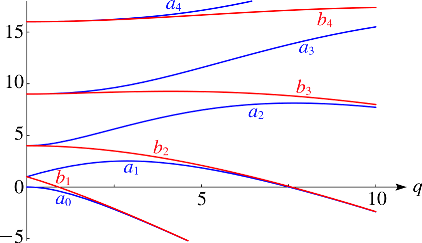 |
|---|
Using Runge-Method to solve the following equation:
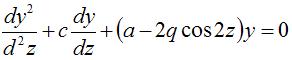 |
|---|
Here I provide some typical solutions:
1. Stability system without damping character a = 0.7, q = 0.2, Y0 = 0, Y0' = 0.5, c =0:
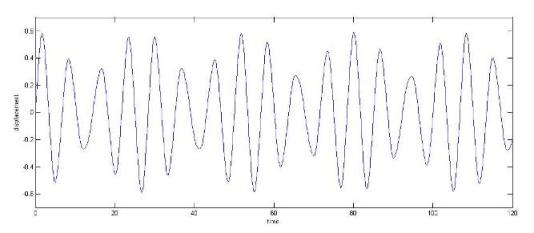 |
|---|
2. Instability system without damping character a = 1, q = 0.1, Y0 = 0, Y0' = 0.5, c =0:
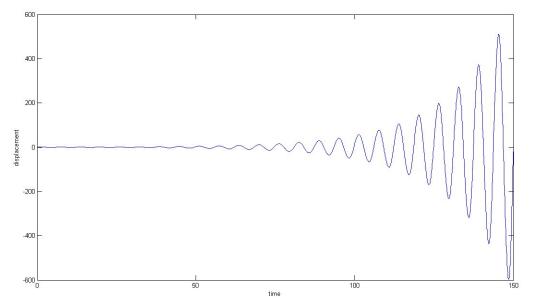 |
|---|
3. Instability system with damping character a = 1, q = 0.1, Y0 = 0, Y0' = 0.5, c =0.05(left) / c = 0.15(right) (Please be aware that the following two graphics have different axial scalar properties):
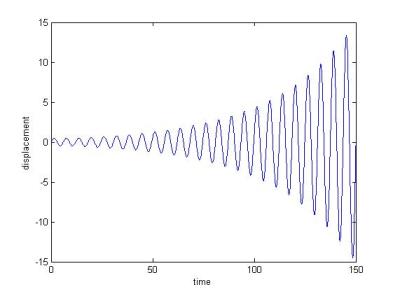 |
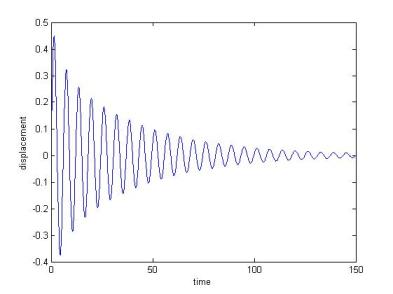 |
|---|
4. Instability system(second order) without damping character a = 4, q = 0.5, Y0 = 0, Y0' = 0.5, c =0:
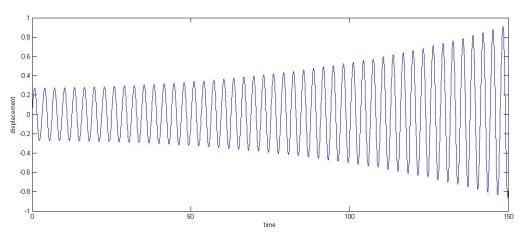 |
|---|
For any advises, problems, etc., please feel free to contact me.